There is a lovely formula for the sum
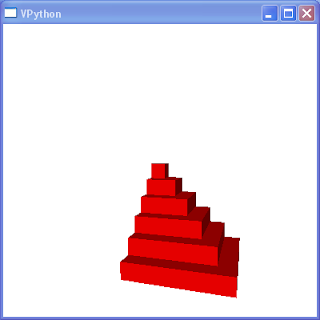
The sum of the first 6 cubes represented as a solid.
Imagine the sum
 |
 |
