There is a lovely formula for the sum $latex S_n$ of the first $latex n$ square integers. Namely
$latex S_n = 1^2 + 2^2 + 3^2 + \ldots + n^2 = \frac{n(n+1)(2n + 1)}{6}.$
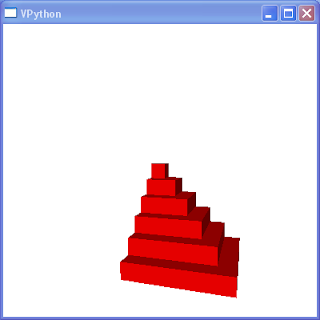
The sum of the first 6 cubes represented as a solid.
Imagine the sum $latex S_n $ as the volume of the pyramid of 1 x 1 x 1 cubes with one cube on the top layer, 4 on the next, 9 on the next and so on up to $latex n^2$ cubes on the bottom layer as seen in the figure above. From the above expression, we see that the sum is one sixth the volume of a box with dimensions $latex n$, $latex n + 1$, and $latex 2n + 1$. So it is at least conceivable that six of these pyramids could be packed into a rectangular volume of that size. And as the pictures indicate below, there is such an arrangement.
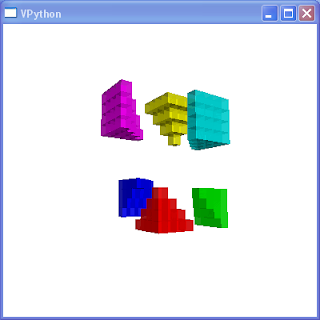 |
 |
With out new CNC router, we thought it would be fun to build a physical model to demonstrate this formula.

Read about my first experience with CNC routing the sum of squares here.

